Supervisory Control under Local Mean Payoff Constraints

Posted on Edited on In
Implementation of algorithms designed by Yiding Ji and Stéphane Lafortune

Abstract

The paper investigates quantitative supervisory control with a local mean payoff objective for weighted discrete event system. The supervisor is designed to ensure that the mean payoff of weights over a fixed number of transitions never drops below a given threshold, aka the system stability. The algorithms transfer the supervisory control problem to a biparty game between the supervisor and the environment.

Automaton Model

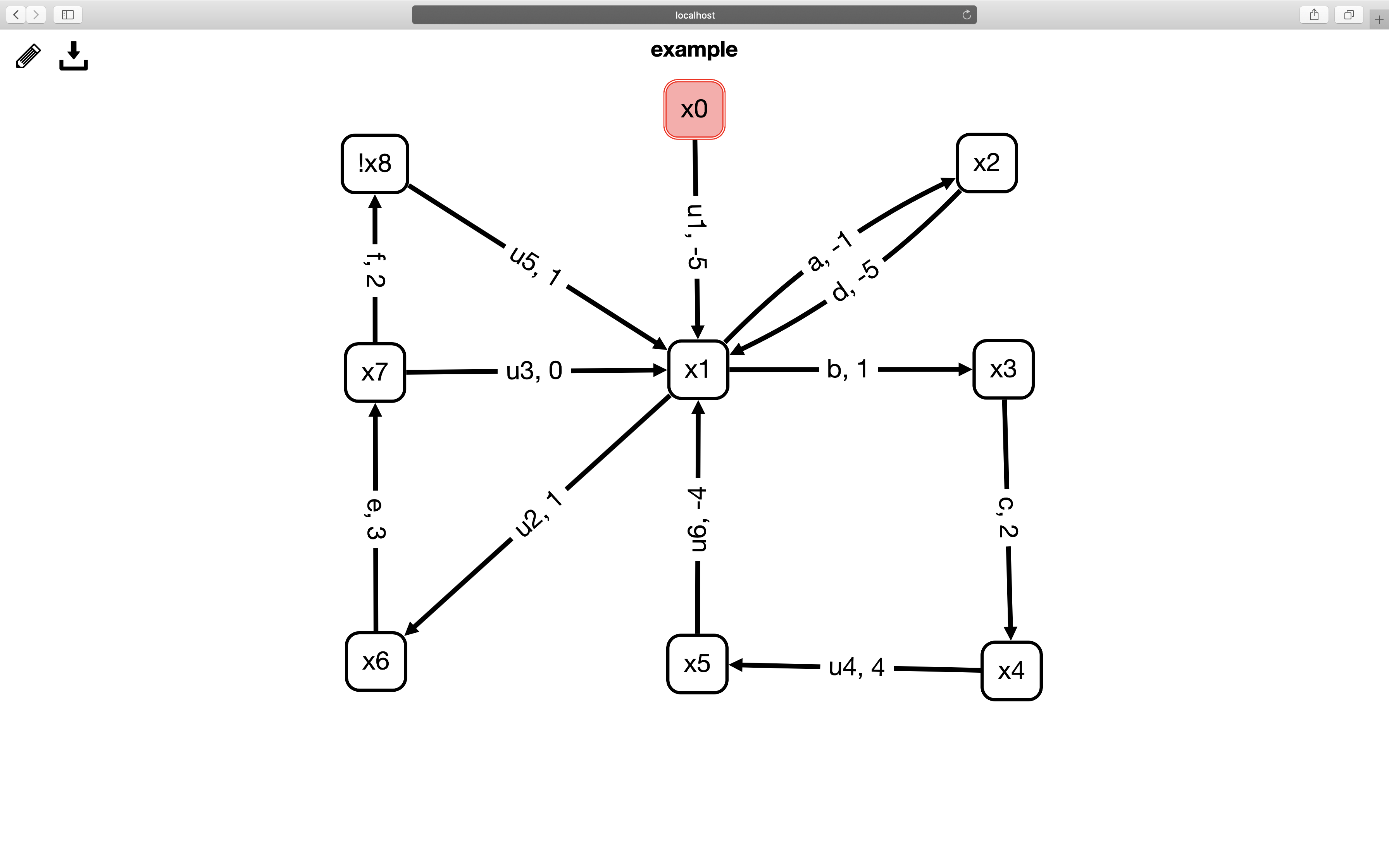
The weighted discrete event system can be modeled as an automaton. Here shows an example. The state with “!” is unsafe ($x_8$). The set of controllable events is $E_c=\{a,b,c,d,e,f\}$, and the set of uncontrollable events is $E_{uc}=\{u_1,u_2,u_3,u_4,u_5\}$. The localhost website gui is supported by the WebMachine from transitions_gui package.

1
2
3
4
5
6
7
8
9
10
def visualizeMachine(states, transitions, initial, name, ordered_transitions=False, ignore_invalid_triggers=True, auto_transitions=False):
    machine = WebMachine(states=states, transitions=transitions, initial=initial, name=name,
                         ordered_transitions=ordered_transitions,
                         ignore_invalid_triggers=ignore_invalid_triggers,
                         auto_transitions=auto_transitions)
    try:
        while True:
            time.sleep(5)
    except KeyboardInterrupt:
        machine.stop_server()

Algorithm 1

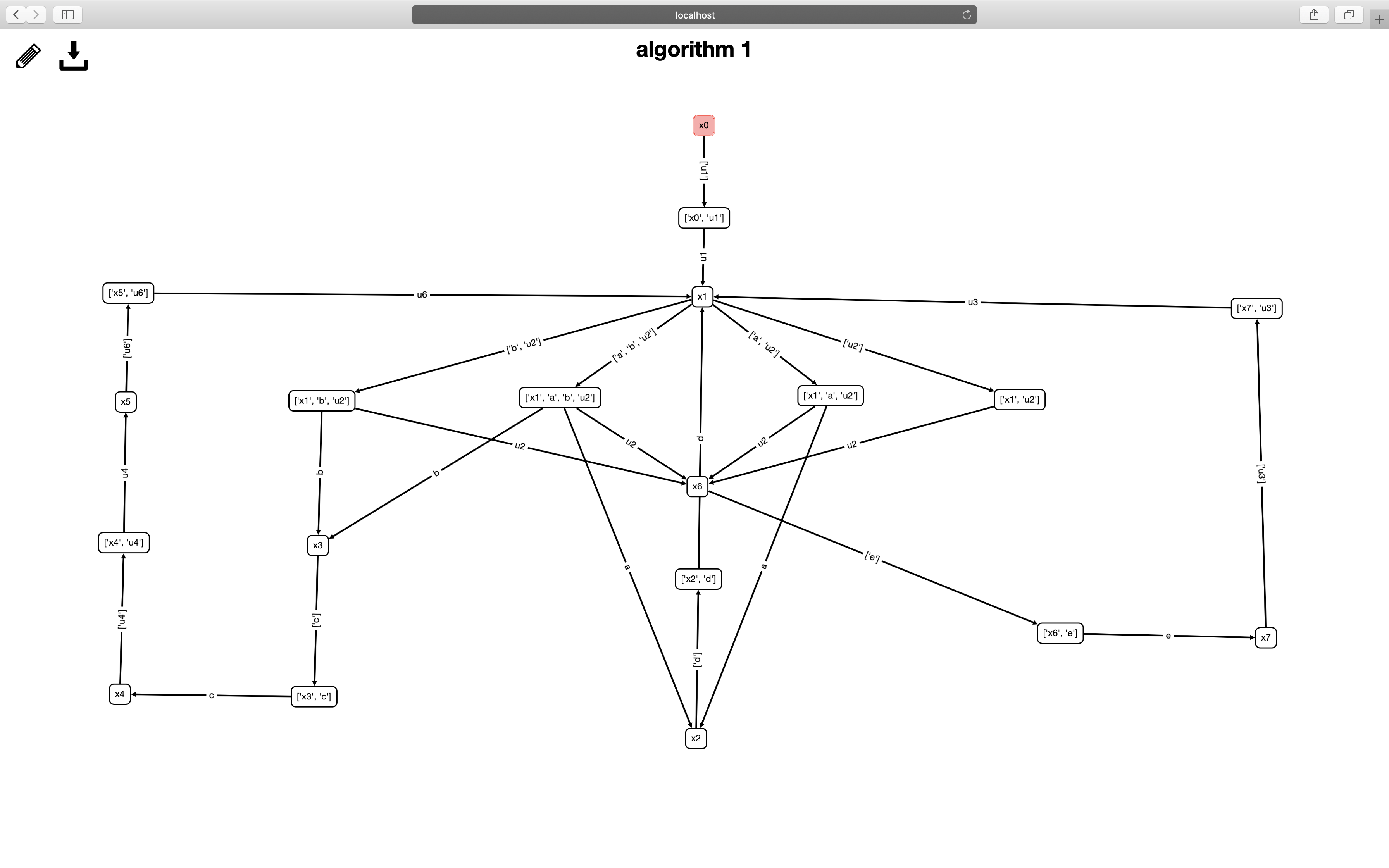
The first algorithm is to transform the automaton model to a biparty game. It has two steps: insert transition states into the original automaton, and remove deadlocking or unsafe states. We can use DFS to find out all transitions, and generally the inserted transition states of one original state are the combination of all controllable events at that state plus the uncontrollable ones.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
def DoDFS(y, X, x0, f, Ec, Euc, w, Qy, Qz, G, fyz, fzy):
    gamma = []
    tEuc = []
    tEc = []
    for t in f:
        if t[1] == y:
            if t[0] in Euc:
                tEuc.append(t[0])
            else:
                tEc.append(t[0])
    if len(tEuc) == 0 and len(tEc) == 0:
        return
    if len(tEuc) != 0 and len(tEc) == 0:
        gamma.append(tEuc)
        G.append(tEuc)
    else:
        if len(tEuc) != 0:
            gamma.append(tEuc)
            G.append(tEuc)
        for i in range(1, len(tEc) + 1):
            l = list(combinations(tEc, i))
            for r in l:
                gamma.append(list(r) + tEuc)
                G.append(list(r) + tEuc)
    for g in gamma:
        z = [y] + g
        fyz.append([g, y, z])
        if z not in Qz:
            Qz.append(z)
            for e in g:
                yn = ''
                for t in f:
                    if t[0] == e and t[1] == y:
                        yn = t[2]
                        break
                if yn[0] == '!':
                    continue
                fzy.append([e, z, yn])
                if yn not in Qy:
                    Qy.append(yn)
                    DoDFS(yn, X, x0, f, Ec, Euc, w, Qy, Qz, G, fyz, fzy)

def removeUnsafe(states, transitions):
    for s in states:
        if s[0] == '!':
            for t in transitions:
                if t[1] == s or t[2] == s:
                    transitions.remove(t)
            states.remove(s)

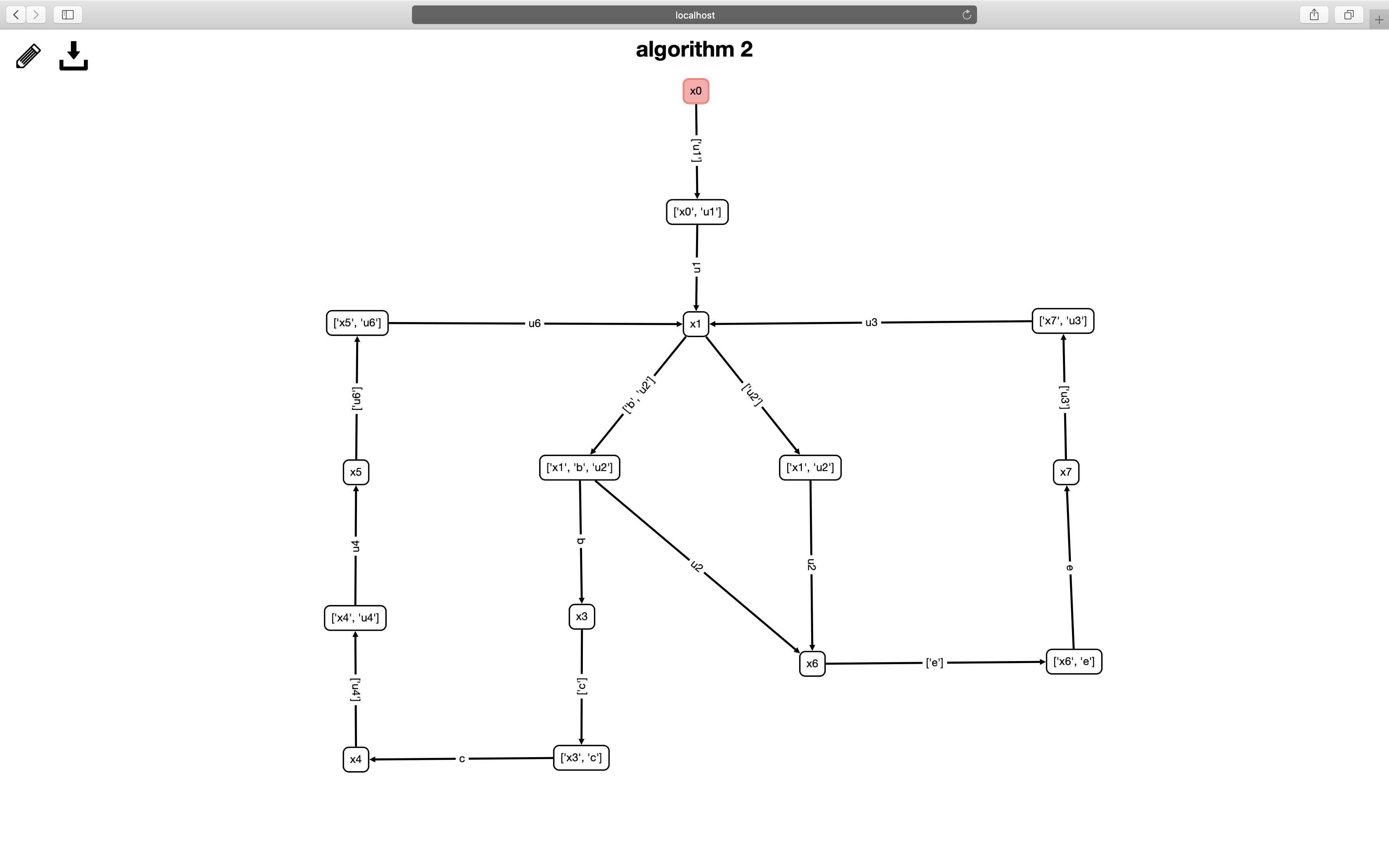
Algorithm 2

The second algorithm is to find the supervisor’s winning region. It first calculates the window mean payoff function which tracks the best worst-case accumulative weights that the supervisor may achieve from a state within N event occurrences (window size). Then the goal equivalents to adopting a control strategy to obtain a nonnegative accumulative payoff while the environment aims to spoil that goal by enforcing negative payoffs. We can use divide-and-conquer to find out all stable windows where the local window mean payoffs are all nonnegative. The example has a window size of three.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
def StableWindow(Qy, Qz, fyz, fzy, w, N):
    wgr = []
    h = {}
    h[0] = {}
    for q in Qy + Qz:
        h[0][str(q)] = 0
    for i in range(1, N+1):
        h[i] = {}
        for q in Qz:
            ey = [[element[0], element[2]]
                  for element in fzy if element[1] == q and element[2] in Qy]
            if len(ey) != 0:
                ystates = []
                for y in ey:
                    if str(y[1]) in h[i - 1].keys():
                        ystates.append(y)
                if len(ystates) != 0:
                    h[i][str(q)] = min([w[t[0]] + h[i - 1][str(t[1])]
                                        for t in ystates])
                    if h[i][str(q)] >= 0:
                        wgr.append(q)
        for q in Qy:
            ytz = [element[2]
                   for element in fyz if element[1] == q and element[2] in Qz]
            if len(ytz) != 0:
                zstates = []
                for z in ytz:
                    if str(z) in h[i].keys():
                        zstates.append(z)
                if len(zstates) != 0:
                    h[i][str(q)] = max([h[i][str(z)] for z in zstates])
                    if h[i][str(q)] >= 0:
                        wgr.append(q)
    wg = []
    [wg.append(q) for q in wgr if not q in wg]
    return wg

def WinLocal(Qy, Qz, fyz, fzy, w, N):
    wg = StableWindow(Qy, Qz, fyz, fzy, w, N)
    wp = []
    if len(wg) == len(Qy + Qz) or len(wg) == 0:
        wp = wg
    else:
        Qyn = []
        for y in Qy:
            if y in wg:
                Qyn.append(y)
        Qzn = []
        for z in Qz:
            if z in wg:
                Qzn.append(z)
        wp = WinLocal(Qyn, Qzn, fyz, fzy, w, N)
    return wp

def attraction(attr, s0, Q, f, wp):
    if s0 in wp:
        return True
    else:
        res = []
        for i in f:
            if i[1] == s0:
                res.append(attraction(attr, i[2], Q, f, wp))
        for i in res:
            if i == False:
                return False
        attr.append(s0)
    return True

def winRegion(Qy, Qz, fyz, fzy, w, N, y0, wl):
    ws = []
    n = 1
    Qyw = [y for y in Qy]
    Qzw = [z for z in Qz]
    while len(ws) != len(Qy + Qz):
        wp = WinLocal(Qyw, Qzw, fyz, fzy, w, N)
        wl += wp
        if len(wp) == 0:
            break
        attrr = []
        _ = attraction(attrr, y0, Qy + Qz, fzy + fyz, wp)
        for p in wp + attrr:
            if p not in ws:
                ws.append(p)
        for y in Qyw:
            if y in ws:
                Qyw.remove(y)
        for z in Qzw:
            if z in ws:
                Qzw.remove(z)
        n += 1
    return ws

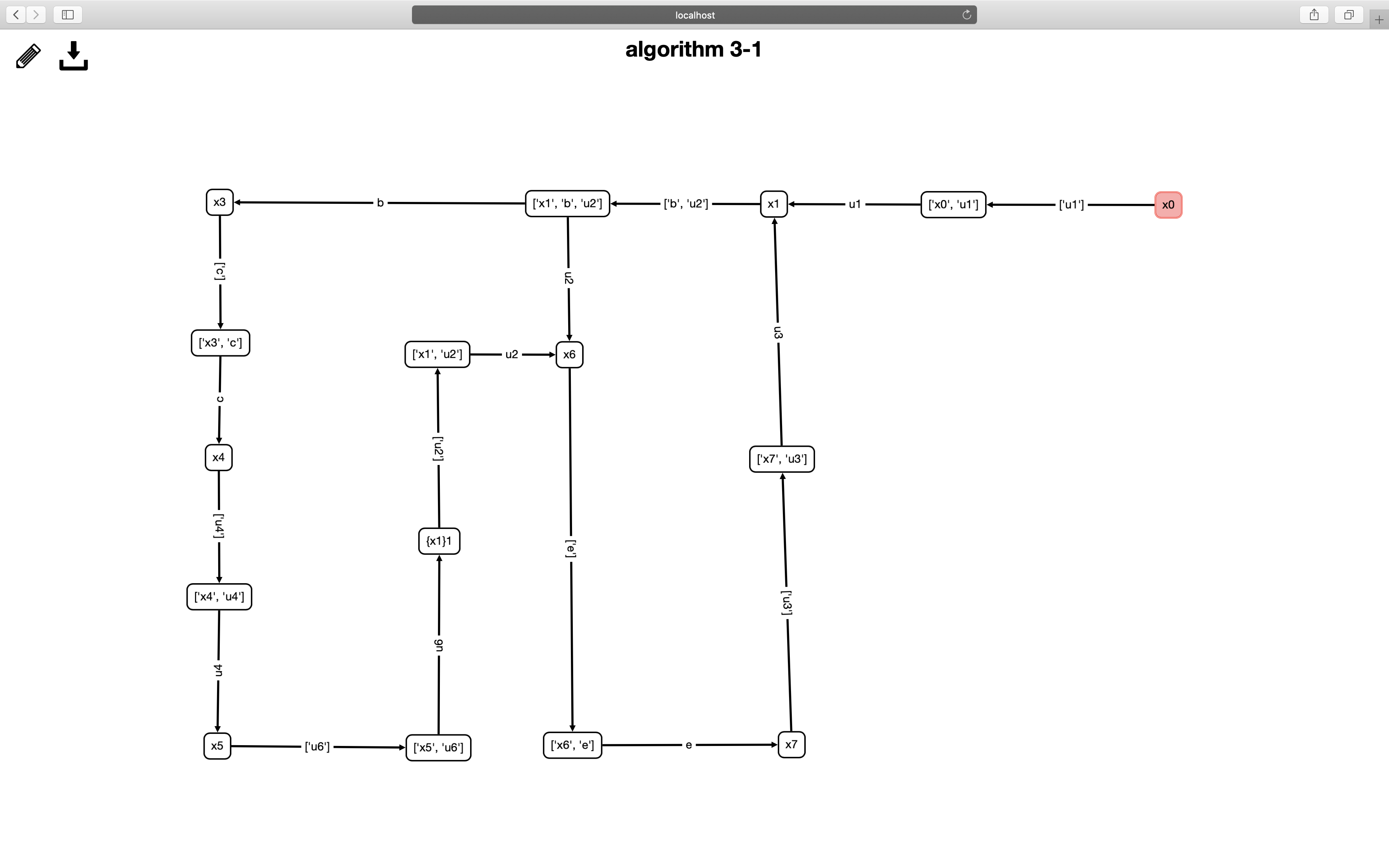
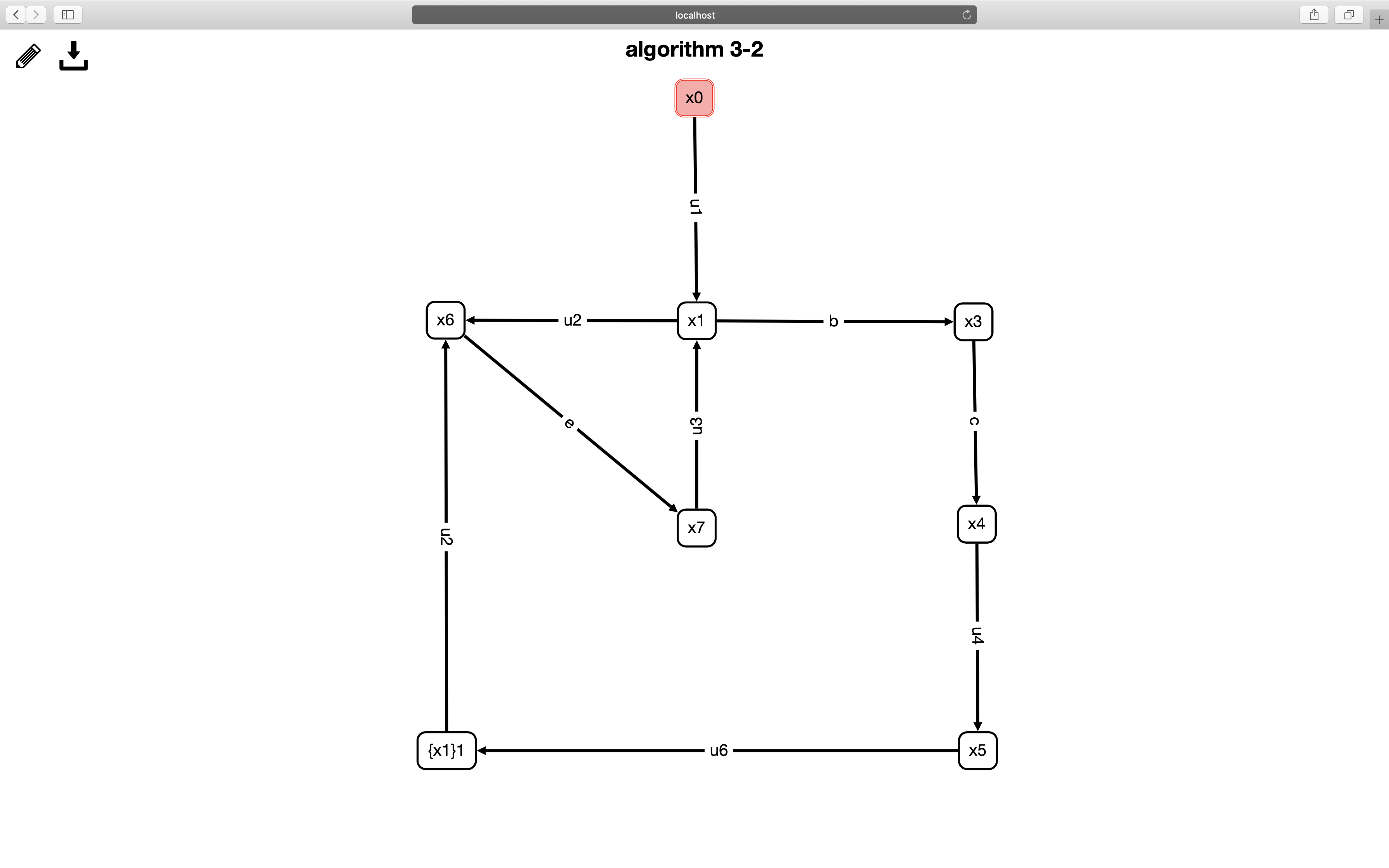
Algorithm 3

The third algorithm is to reconstruct and unfold the result of the second algorithm. It has two steps. The first one is to merge all stable windows in the second algorithm together, and add original states back to the automaton so that each original state has only one transit-out arrow. The second one is to remove all the inserted environment states to simplify the automaton and finally give a stable workflow.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
def Unfold(y0u, Qyu, Qzu, fyzu, fzyu, Qy, Qz, fyz, fzy):
    duplicate = {}
    lru = {}
    for i in Qy:
        duplicate[i] = 1
        lru[i] = 0
    state = y0u
    while len(Qzu) < len(Qz):
        du = False
        sn = ''
        if state in Qyu:
            if duplicate[state] != 1:
                du = True
                sn = '{'+state+'}'+str(lru[state])
                if lru[state] != 0:
                    Qyu.append(sn)
        else:
            Qyu.append(state)
            d = 0
            for i in fyz:
                if i[1] == state:
                    d += 1
            duplicate[state] = d
        lru[state] = (lru[state] + 1) % duplicate[state]
        temp = []
        for i in fyz:
            if i[1] == state and i[2] not in Qzu:
                temp.append(i)
        z = ''
        if len(temp) == 1:
            z = temp[0][2]
            Qzu.append(z)
            if du == False:
                fyzu.append(temp[0])
            else:
                fyzu.append([temp[0][0], sn, z])
        else:
            t = [len(i[2]) for i in temp]
            yz = temp[t.index(max(t))]
            z = yz[2]
            Qzu.append(z)
            if du == False:
                fyzu.append(yz)
            else:
                fyzu.append([yz[0], sn, z])
        y = []
        for i in fzy:
            if i[1] == z:
                if lru[i[2]] == 0:
                    fzyu.append(i)
                else:
                    fzyu.append([i[0], i[1], '{'+i[2]+'}'+str(lru[i[2]])])
                y.append(i[2])
        if len(y) == 1:
            state = y[0]
        else:
            yin = []
            for i in y:
                if i not in Qyu:
                    yin.append(i)
            num = []
            if len(yin) == 0:
                for i in y:
                    count = 0
                    for j in fzy:
                        if j[2] == i:
                            count += 1
                    num.append(count)
                state = y[num.index(min(num))]
            else:
                for i in yin:
                    count = 0
                    for j in fzy:
                        if j[2] == i:
                            count += 1
                    num.append(count)
                state = y[num.index(min(num))]